Description
115 MATH COMMON CORE ALIGNED QUESTIONS TO TRANSFORM YOUR CLASSROOM! Perfect for morning work, math rotations, spiral review, and math practice!
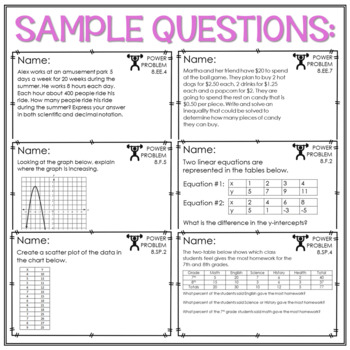
5 questions per standard/topic!
Standards & Topics Covered
Functions
➥ 8.F.1 – Understand that a function is a rule that assigns to each input exactly one output
➥ 8.F.2 – Compare properties of two functions each represented in a different way
➥ 8.F.3 – Interpret the equation y = mx + b as defining a linear function, whose graph is a straight line
➥ 8.F.4 – Construct a function to model a linear relationship between two quantities
➥ 8.F.5 – Describe qualitatively the functional relationship between two quantities by analyzing a graph
The Number System
➥ 8.NS.1 – Understand that every number has a decimal expansion
➥ 8.NS.2 – Use rational approximations of irrational numbers
Expressions and Equations
➥ 8.EE.1 – Develop and apply the properties of integer exponents to generate equivalent numerical expressions
➥ 8.EE.2 – Square and cube roots
➥ 8.EE.3 – Use numbers expressed in scientific notation to estimate very large or very small quantities and to express how many times as much one is than the other.
➥ 8.EE.4 – Perform multiplication and division with numbers expressed in scientific notation to solve real-world problems
➥ 8.EE.5 – Graph proportional relationships, interpreting the unit rate as the slope of the graph
➥ 8.EE.6 – Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane
➥ 8.EE.7 – Solve linear equations in one variable
➥ 8.EE.8 – Analyze and solve pairs of simultaneous linear equations
Geometry
➥ 8.G.1 – Verify experimentally the properties of rotations, reflections, and translations
➥ 8.G.2 – Using transformations to define congruency
➥ 8.G.3 – Describe the effect of dilations about the origin, translations, rotations about the origin in 90 degree increments, and reflections across the -axis and -axis on two-dimensional figures using coordinates.
➥ 8.G.4 – Use transformations to define similarity.
➥ 8.G.5 – Use informal arguments to analyze angle relationships.
➥ 8.G.6 – Explain the Pythagorean Theorem and its converse.
➥ 8.G.7 – Apply the Pythagorean Theorem and its converse to solve real-world and mathematical problems.
➥ 8.G.8 – Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
➥ 8.G.9 – Understand how the formulas for the volumes of cones, cylinders, and spheres are related and use the relationship to solve real-world and mathematical problems.
Statistics and Probability
➥ 8.SP.1 – Interpreting line plots
➥ 8.SP.2 – Understanding Bivariate quantitative data
➥ 8.SP.3 – Use the equation of a linear model to solve problems in the context of bivariate quantitative data, interpreting the slope and y-intercept.
➥ 8.SP.4 – Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table.
WHAT ARE P.O.W.E.R PROBLEMS?
PURPOSEFUL – These problems are meant to keep students focused, while strengthening initiative and perseverance.
OPPORTUNITIES – These prompts can be used in a variety of ways. P.O.W.E.R problems can be used to introduce a lesson, spiral review, or as formative assessments.
WITH
ENGAGEMENT – Problems are real world applicable and designed to hook students with interest and presentation. Complexity of problems promotes problem solving skills.
RIGOR – Tasks are specifically designed to challenge students and assess conceptual understanding of curriculum versus procedural understanding. Students will need to apply more than just a “formula.”
WHY USE P.O.W.E.R PROBLEMS?
BUILD STAMINA WITHIN YOUR STUDENTS!
P.O.W.E.R problems are designed to challenge your students with their open ended presentation. Majority of problems that come from textbooks and workbooks assess procedural understanding of curriculum. Some textbooks even provide step by step instructions where the textbook is thinking for the students and taking away that “productive struggle” for children. When we rob students of that event, we rob them of their ability to reason, problem solve, and see beyond a standard algorithm. P.O.W.E.R problems are meant to show students that there are different ways to answer one question in math. With these tasks students take ownership and are part of the problem solving process versus filling in blanks in a textbook.
HOW TO USE POWER PROBLEMS:
YOUR KIDS. YOUR CHOICE. FLEXIBILITY.
TO INTRODUCE A LESSON – P.O.W.E.R problems can be used to introduce a new skill. In this case your students will experience a “productive struggle.” Their problem solving skills and prior knowledge will kick in. Often times most of my students will have the incorrect answer or no answer at all. I then have someone explain their method/reasoning and allow my students to critique their peer’s answer. This makes for great accountable talk discussions. If I see that most students do not have an answer I will assist the class in getting to a specific point and then allow them to finish independently.
SPIRAL REVIEW – Avoid your students forgetting standards, by using P.O.W.E.R problems to spiral review previously taught lessons.
FORMATIVE ASSESSMENTS – You can use these problems to assess mastery and levels of understanding.