
One of the foundations for understanding mathematics for students is knowing and recognizing the differences between single-digit numbers, teen numbers, and multiples of ten. As an adult, this concept seems very simple, but it must be explicitly taught to our youngsters in order for them to be able to apply the concept later in their math careers.
This is a great opportunity to bring out your base-ten blocks. You will want to have a stockpile of them so that your students can work in small groups and even partnerships to promote discussion during this crucial learning time.
Day 1
On the first day of instruction, show the students the ones blocks. You can gather them in a group or use a document camera to show them the block. Tell them you are going to count together to 100 using the ones blocks (only). Have them choral count with you to twenty or so, bringing in one more block for each number.
You may start acting fatigued because it is taking so long to count by ones. Have a group discussion about how long it would take to count to 100 using only those tiny little blocks and see if they have any ideas. You can ask some prompting questions, or just let their ideas flow. This is when the magic happens and you introduce our friend, the tens rod.
Have a couple of students come up to examine the tens rod to make sure that it is indeed composed of ten little blocks. Line up ten ones blocks next to the rod so that they can see that they are an equal amount. You may even have them give you a “thumbs up” if they agree that they are equal and we could count using those instead.
To end this exploratory lesson, have a class discussion about the names of these manipulatives. Make sure they know that the “mathematical terms” are ones and tens or ten rods, but we’re talking with students in primary grades, and the mathematical terms don’t always give them the concrete foundation that they need. To help with this, begin drafting names for the manipulatives with your class. Use prompts like:
What does it look like?
What do they remind you of?
What is a more fun name for this?
Most kids come up with French fries for tens and tater-tots for ones. Some even come up with cheese sticks and cheese cubes. It will depend on your class, but make a list that is visible for everyone and tell them that the next day, they will take a vote on the names that they’ll use for the manipulatives in class. My students prefer to use cheese cubes and French fries, which does not make sense to me since they aren’t even in the same food group, but they don’t have any problems transforming cheese into potatoes, so let the imaginations run wild!
Day 2
On the second day, kick off your lesson with a really exciting class vote on what to call your ones cubes and ten rods. This will help with the vocabulary moving forward because it can be confusing for kids to hear and understand the statement “Let’s trade in 10 ones blocks for a ten rod.” It’s much easier for them to understand and picture “Let’s trade in 10 cheese cubes for a cheese stick.” The image they create in their minds is much clearer, which helps them in the long run.
I was pretty hesitant at first to provide the students with an alternative name for these manipulatives because I wanted them to know what they represented rather than just a cute substitution, but it really works! Note that you will not always refer to these manipulatives by the voted-on name, but it provides them with the mental image that they need moving forward.
After voting on names for your manipulatives, introduce your students to a place value mat. Most mats use three place values, but for the purpose of this lesson, you should use mats with two place values (tens and ones). I refer to the two place value columns as “houses” and use the language that each manipulative “lives” in its own house; they cannot share. This prepares them for trading ones for tens and for adding and subtracting using manipulatives.

Have a discussion with the students about where they think each manipulative would go on the mat and why. Some prompting questions you can use are:
Which is worth more – a cheese cube or a cheese stick? How do you know?
Where would we put the “cheese cubes” and where would we put the “cheese stick”? Why would we put them in that order?
What could we do if we have too many cheese cubes in the house?
Eventually, you want your students to come to the conclusion that the tens go on the left and ones go on the right.
End this lesson by writing a couple of single-digit numbers on the board and having the students demonstrate with their manipulatives how much that is. For example, if you write the number 8 on the board, the students should count out 8 “cheese cubes” into their “cheese cube house”.
Day 3
Begin this lesson with a review of the name the class chose for the manipulatives and another single-digit practice number on the board.
Today, you will introduce the students to using the manipulatives and place value mat for counting teen numbers.
Give each student a “cheese stick” and 19 “cheese cubes” to start the lesson along with their place value mat.
Write a teen number on the board and demonstrate how to build it, counting one block at a time until you get to the number. Ask the students what you could trade in 10 “cheese cubes” for now. They should exclaim “cheese stick” (or whatever name they gave to the ten rod). Go ahead and trade the 10 blocks for a rod, lining them up next to each other so they can see. Allow them to also count how many “cheese cubes” are left in the ones column along with how many “cheese sticks” are in the tens column.
Give students multiple opportunities to practice this activity with different teen numbers. After a few trials, see if they recognize the pattern of having one “cheese stick” every time there is a teen number. Prompt them to start with the “cheese stick” counting it as ten and then counting on to finish the teen number. You may need to model this a couple of times before they are ready to try it.

To end the lesson, model a few teen numbers using the manipulatives and have the students determine what number you created. For example, if you model one “cheese stick” and 5 “cheese cubes”, the students should be able to say that you made the number 15. Try this a few times to see if they can recognize that the “cheese stick” is worth 10 and they can count on to make the teen number.
Day 4
Begin this lesson with another review of what they did in the previous lesson. Provide modeled examples of teen numbers as well as writing teen numbers to allow them to create the model with their manipulatives. Continue to use the terms they voted on and interchange those terms with the mathematical terms (ones and tens).
Now for the fun part… Introduce a game called “Trade Up” to the students. This game can be played individually or in pairs. It is usually more fun to start out in pairs for this game, and it requires fewer materials, which is an extra bonus.
Give each student their own place value mat, 2 ten rods, and 15 ones blocks. (I give them 15 ones blocks so that if they have 9 ones and roll a 6, they can build the number before trading in 10). Give each pair one 6-sided die. The pair will take turns rolling their die and putting that many ones blocks on their place value mat. When they reach 10 (or more), they should trade up for a tens rod. Their goal is to make it to 20 before their partner. Of course, this is really a game of luck, but it does provide a little more fun to their practice of counting and trading ones for tens, which will help them in the long run.
This game can be played fairly quickly once your students get the hang of it. You can turn it into a tournament, where the pairs keep track of how many “Trade Up” games they have won with tally marks. For students who do not do well with competition, I have them compete against themselves to see how few rolls they can have to make 20 or have them time themselves when they really get fluent with the process.
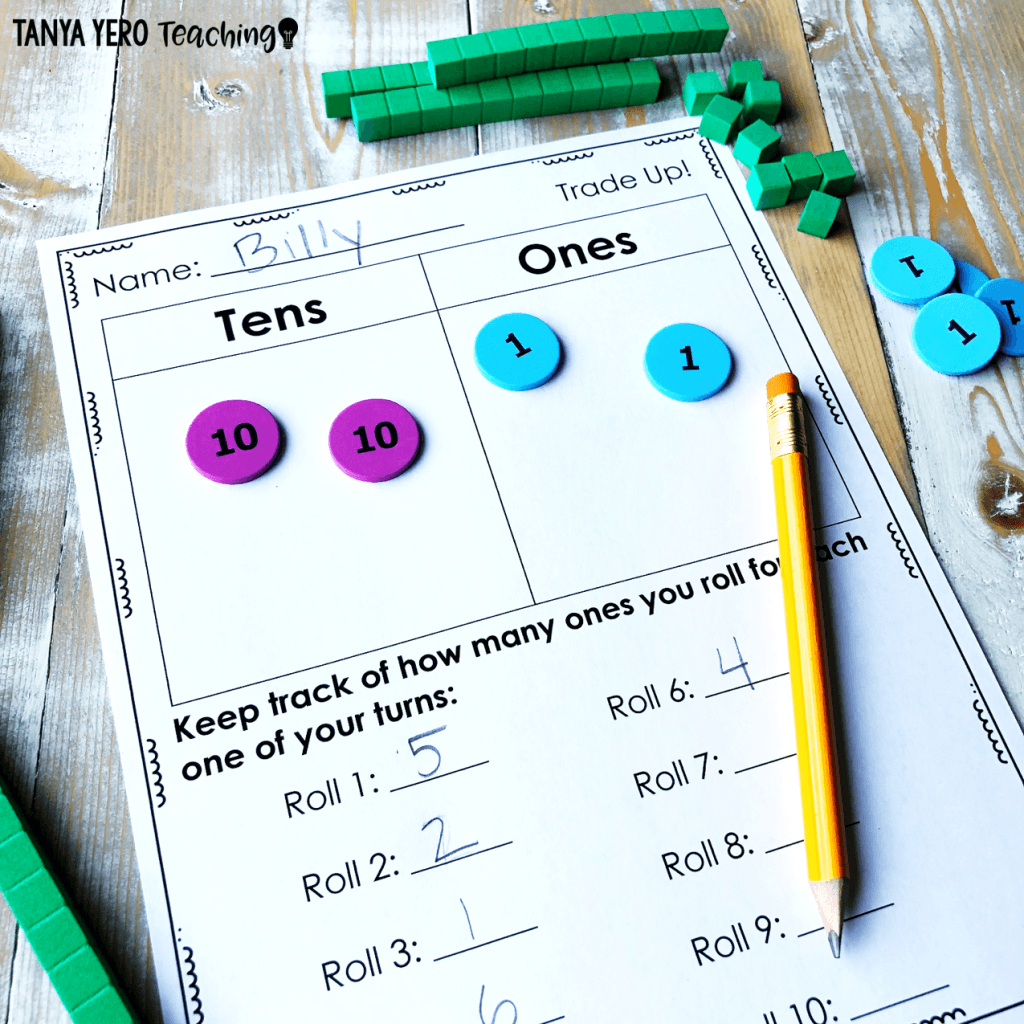
Another thing I love about this game is that it is very easy to differentiate. For students who are having a difficult time counting up and trading, you can provide a ten-frame within the place value chart. This way, they know that when the ten-frame is full, they should trade for a rod. Remind them that rods live in the “cheese stick” house and not in the “cheese cube” house.
For students who master this fairly quickly, you can have them trade up to a higher number. Just make sure they have enough tens rods to continue to trade up to that number. I suggest having them trade up to 50 to start with.
As your students progress, this type of activity can be used to help them count by tens, add and subtract double-digit numbers, and the list can go on.
Sign up below for your FREE templates that are pictured in this blog post!
Success! Now check your email to confirm your subscription. YOU'RE SO CLOSE TO YOUR FREE MATH ACTIVITY!
SIGN UP FOR YOUR FREE RESOURCE!
SUBSCRIBE NOW TO OUR NEWSLETTER TO RECEIVE YOUR FREE PRINTABLES!
GET YOUR TEMPLATES HERE!







